Фибоначчи – это не просто имя математика, это целая система чисел, которая встречается в природе, искусстве и финансах. Чтобы понять, как эти числа работают и почему они так важны, важно изучить биографию и факты о Леонардо Пизанском, известном как Фибоначчи.
Биография Фибоначчи
Фибоначчи появился на свет ок. 1170 года в городе Пиза. Его отец, Гильермо, зарабатывал на жизнь торговым промыслом. Когда в 1192 г. ему доверили представлять пизанскую торговую колонию в Северной Африке, он часто бывал в разных странах.
Желая, чтобы сын пошел по его стопам, отец позвал Фибоначчи в
Алжир. В этой стране юноша обучался математике у арабских преподавателей. Он ознакомился с достижениями греческих и индийских математиков, после чего вернулся домой.
Мнение эксперта:
Фибоначчи – это последовательность чисел, в которой каждое последующее число равно сумме двух предыдущих. Эта математическая последовательность имеет широкое применение в различных областях, включая финансы, искусство и природу. Эксперты отмечают, что Фибоначчи-числа используются в техническом анализе финансовых рынков для прогнозирования ценовых уровней. Они также играют важную роль в искусстве, архитектуре и музыке, вдохновляя творческие решения и создавая гармонию. В природе Фибоначчи-последовательность можно увидеть в строении растений, раковин моллюсков и во многих других биологических объектах. Эксперты подчеркивают, что Фибоначчи-числа имеют удивительные свойства, которые продолжают вдохновлять исследователей и творцов в различных областях.

Научная деятельность
Приехав в Пизу Фибоначчи приступил к написанию «Книги абака», которая считается его главным наследием. В ней автор излагал и популяризировал десятичную арифметику, которая была ему хорошо знакома по ряду арабских трудов.
Важно отметить, что «Книга абака» была написана ясным языком и рассчитана для тех, кому требовались практические подсчеты – первоначально для торговцев. Этот труд, благодаря простому и глубокому изложению, превосходил все античные и арабские прототипы.
По этой причине книга считалась непревзойденной, почти до времен
Декарта, жившего в 17 веке. Обладая большими знаниями, которые он получил от арабских учителей, Фибоначчи написал множество математических трактатов, которые представляли огромную ценность для западноевропейской науки той эпохи.
Ведь благодаря книге Фибоначчи, в Европе началось распространение позиционной системы исчисления, которая была гораздо удобнее, нежели римская. Автор доходчиво обосновывал практичность употребления арабских чисел, наряду с другими системами вычислений. К слову, почти каждое свое утверждение он сопровождал веским доказательством.
Интересен факт, что «Книга абака» обратила на себя пристальное внимание самого императора Фридриха II. Правитель Римской империи пригласил Фибоначчи к себе на прием, на котором математику задавали разные вопросы и задачи его придворные.
В последующие годы биографии Фибоначчи пользовался большим уважением и покровительством Фридриха. В 1220 г. он издал книгу «Практика геометрии», в которой были представлены ряд теорем с доказательствами, касающихся измерительных методов.
Спустя 5 лет свет увидел очередной научный труд ученого «Цветок». На этот раз Фибоначчи занимался изучением кубических уравнений. Тогда же он опубликовал еще одну значимую работу – «Книга квадратов». В ней содержалось множество задач в области неопределенных квадратных уравнений.
Математик искал числа, которые, будучи добавленными к квадратному числу, снова дадут квадратное число. В 1240 г. он удостоился пенсии за заслуги перед городом. За годы биографии Фибоначчи часто принимал участие в разных математических соревнованиях.
Любопытно, что в своих книгах ученый нередко представлял самые различные виды задач, а также решения к ним с подробными пояснениями. Позднее эти задачи будут печататься во многих учебниках и пересказываться из уст в уста. Отдельного внимания заслуживают так называемые – «Числа Фибоначчи».
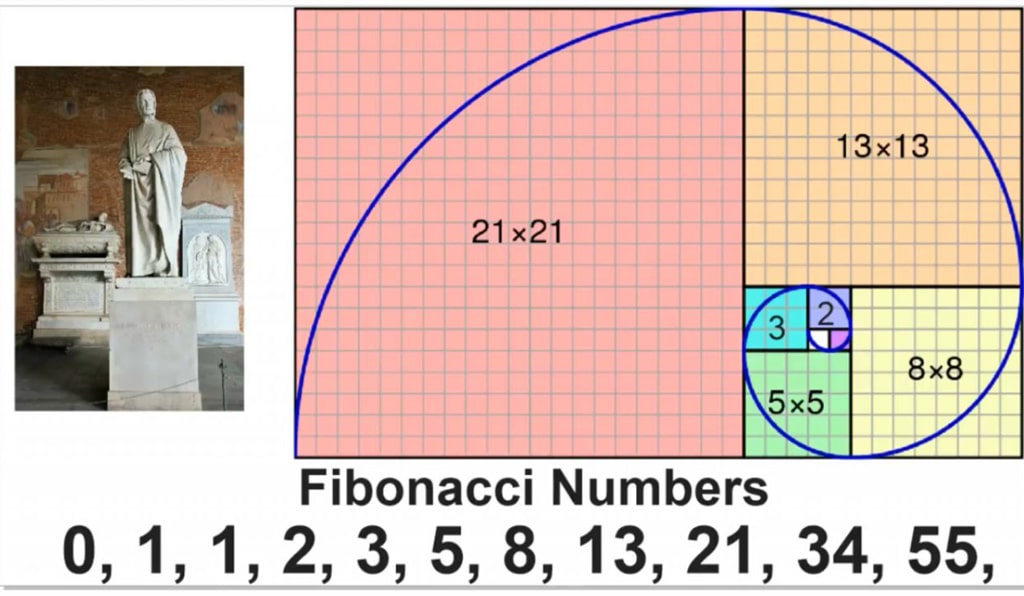
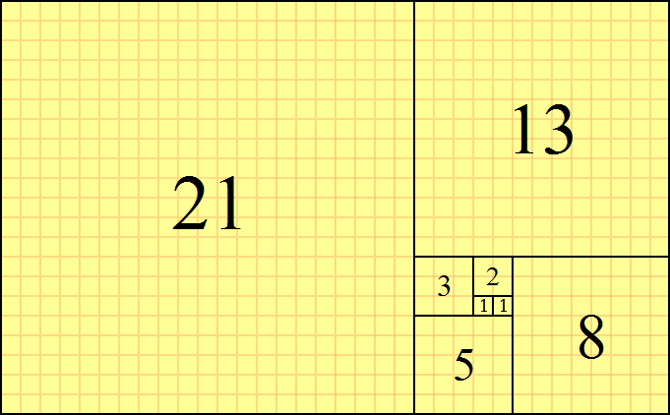
Числа Фибоначчи – элементы числовой последовательности, где первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел:
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + 3 = 5
- 3 + 5 = 8
- 5 + 8 = 13 и т. д.
Числа Фибоначчи актуальны во многих сферах математики. До нас не дошло ни одного прижизненного портрета ученого, поэтому все известные сегодня являются лишь современными представлениями о нем. Также математик не оставил после себя фактически никаких автобиографических сведений.
Интересные факты
- Числа Фибоначчи встречаются в природе:
- Последовательность чисел Фибоначчи можно увидеть в строении ракушек, лепестков цветов, листьев и даже в расположении звезд в некоторых галактиках.
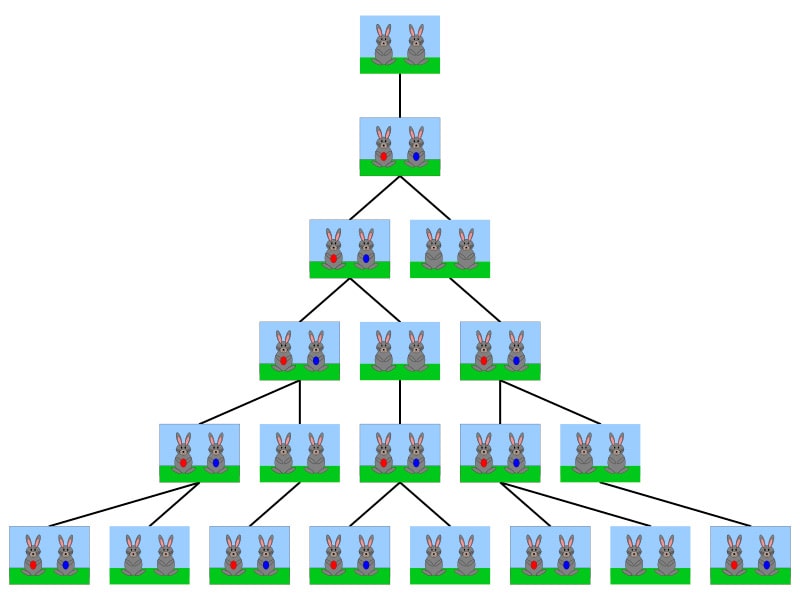
- Числа Фибоначчи также можно увидеть в развитии и росте животных и растений. Например, в строении человеческого тела, пропорции которого соответствуют числам Фибоначчи.
- Числа Фибоначчи использовались в математике и искусстве на протяжении веков:
- Числа Фибоначчи впервые описал индийский математик Пингала в 200 году до нашей эры. Позже их популяризировал итальянский математик Леонардо Фибоначчи в своей книге «Liber Abaci» в 1202 году.
- Числа Фибоначчи использовались в архитектуре, живописи и музыке. Например, в архитектуре они использовались для создания пропорциональных и гармоничных форм, в живописи – для создания композиций, а в музыке – для создания ритмических структур.
- Числа Фибоначчи связаны с золотым сечением:
- Золотое сечение – это особое математическое соотношение, которое часто встречается в природе и искусстве. Числа Фибоначчи являются частью последовательности, которая приближается к золотому сечению.
- Золотое сечение примерно равно 1,618. Это соотношение часто используется в дизайне, архитектуре и искусстве, чтобы создать более эстетически приятные и гармоничные композиции.

Смерть
Точная дата смерти Фибоначчи, как и дата его рождения, остается неизвестной. Леонардо Пизанский (Фибоначчи) умер ок. 1170 года, оставив после селя заметный след в науке.
| Номер | Число Фибоначчи | Примеры в природе |
|---|---|---|
| 1 | 1 | Количество лепестков в большинстве цветов |
| 2 | 1 | Количество глаз у большинства млекопитающих |
| 3 | 2 | Количество камер в сердце человека |
| 4 | 3 | Количество листьев в большинстве деревьев |
| 5 | 5 | Количество пальцев на руке человека |
| 6 | 8 | Количество лепестков в цветке лилии |
| 7 | 13 | Количество листьев в спирали на стебле ананаса |
| 8 | 21 | Количество чешуек в ананасе |
| 9 | 34 | Количество спиц в колесе велосипеда |
| 10 | 55 | Количество листьев в спирали на стебле подсолнуха |
Опыт других людей
Фибоначчи – это не просто математическая последовательность, это источник вдохновения для многих. Люди говорят, что Фибоначчи помогает им понять гармонию природы, отношения в искусстве, а также применять его в торговле на финансовых рынках. Многие отмечают, что использование чисел Фибоначчи в техническом анализе помогает им принимать более обоснованные решения. Также Фибоначчи часто ассоциируется с золотым сечением и гармонией, что делает его популярным среди любителей философии и дизайна.

Фото Фибоначчи
Если вам понравилась краткая биография Фибоначчи – поделитесь ею в соцсетях.
Частые вопросы
В чем смысл чисел Фибоначчи?
Числа Фибоначчи (строка Фибоначчи) — числовая последовательность, первые два числа которой являются 0 и 1, а каждое последующее за ними число является суммой двух предыдущих. Представляет собой частный пример линейной рекуррентной последовательности (рекурсии).
Где в жизни встречаются числа Фибоначчи?
Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи.
Как работает метод Фибоначчи?
Метод Фибоначчи (англ. Fibonacci method) — это улучшение реализации поиска с помощью золотого сечения, служащего для нахождения минимума/максимума функции. Подобно методу золотого сечения, он требует двух вычислений функции на первой итерации, а на каждой последующей только по одному.
Полезные советы
СОВЕТ №1
Изучите историю и принципы работы последовательности Фибоначчи, чтобы понять ее значение и применение в различных областях.
СОВЕТ №2
Попробуйте создать свои собственные числовые последовательности, используя правила Фибоначчи, чтобы лучше усвоить их структуру и свойства.
СОВЕТ №3
Исследуйте применение последовательности Фибоначчи в финансах, искусстве, природе и других областях, чтобы увидеть ее широкий спектр применения.